Las antenas de parche o microstrip son antenas que proceden de la tecnología conocida como. Sin embargo, no deben confundirse dichos términos. Una antena microstrip, es aquella antena que posee una alimentación mediante una línea microstrip; sin embargo, una antena de parche es aquella cuya geometría procede una línea microstrip y que se compone de al menos los siguientes tres componentes:
Plano de masa inferior.
Sustrato por encima de dicho plano de masa.
Un elemento radiante que se sitúa justo encima de dicho sustrato.
Alimentación:
La alimentación de una antena de parche, puede realizarse mediante una línea microstrip, pero existen otras técnicas de alimentación:
alimentación mediante una conexión coaxial.
alimentación mediante una línea stripline.
alimentación mediante una ranura.
alimentación mediante una guia de ondas coplanar.
alimentación mediante una ranura acoplada.
alimentación mediante otra antena de parche por acoplo.
Una antena microstrip es un tipo de antena que usa para procesar señales de frecuencia muy altas. Se suele usar como un receptor para los teléfonos móviles o para sistemas de satélite. Suelen ser las que se montan en aviones o incluso naves que van al espacio. Este tipo de antena tiene la ventaja de que no cuesta mucho fabricarla, aunque también tiene el inconveniente de que tiene una ancho de banda limitado. Como la mayoría sabrá, una antena es un dispositivo diseñado para transmitir y recibir ondas electromagnéticas. Se usa en equipos de radio para convertir ondas de radio en corrientes eléctricas y viceversa.
La única diferencia entre una antena que transmite y una que recibe es la dirección en la que viaja la señal. Una antena microstrip se usa para transmitir y recibir señales en las frecuencias muy altas. El tipo más común es la antena de parche, la cual es rectangular y puede ponerse en superficies planas. Se fabrica poniendo la antena en una cobertura de metal junto con una capa aislante, que puede ser plástico, cerámica, vidrio o ciertos tipos de cristal. El resultado no es demasiado sólido pero consigue un mejor ancho de banda, lo cual significa que puede procesar más información de una sola vez.
Una antena microstrip puede también ser puesta directamente en un circuito integrado. Al requerir estos dispositivos menos materiales para su fabricación, el coste es menor, es más fácil de hacer y es mucho más ligero. Todos estos elementos han hecho de las antenas microstrip ideales para usar en móviles y otros dispositivos electrónicos de pequeño tamaño.
El tamaño de estas antenas es inversamente proporcional a su frecuencia. Esto significa que cuanto más grande sea la antena, más baja será la frecuencia que es capaz de detectar. Por esta razón, se usan normalmente para frecuencias altas. Una antena microstrip capaz de detectar frecuencias más bajas sería demasiado grande para ser usada.
El concepto de este tipo de antena fue propuesto en los años cincuenta, pero no empezó a ser usado de forma real hasta los años setenta. Esto fue porque varios materiales que se usan para el aislante se perfeccionaron bastante y fue viable usarlos con esta tecnología. De todos modos, se siguen haciendo investigaciones para mejorar este tipo de antenas. Varios grupos de ingeniería en compañías conocidas buscan manteas de reducir el tamaño de las antenas microstrip para que los usuarios puedan usar dispositivos aun más pequeños. Por tanto, es una tecnología en constante evolución.
continuara...
20 oct 2017
15 oct 2017
Ley Naranja
El pasado 26 de abril, el partido de Centro Democrático colombiano consiguió la aprobación de una nueva ley de protección de la economía creativa. Fue propuesta por el senador Iván Duque y aprobada por 80 votos a favor y 5 en contra.
Las
industrias culturales están aumentando su fuerza dentro de la economía
de Colombia. En la actualidad, representan un 3% del PIB, siendo un
porcentaje mayor del que ocupan otros sectores, de gran importancia
histórica, como el café y la minería. Además, se trata de una economía
menos volátil que ha soportado mejor los momentos de crisis económica.
Esto
es debido a una población demográfica joven que consume bienes de
entretenimiento, necesitando menos los servicios básicos de asistencia
social. La importancia de las industrias creativas son justificadas en
la ley, debido a la imposibilidad de competir con los bajos costes
asiáticos, y la visión de una caída en los crecimientos de
industrialización y urbanización.
Las industrias creativas
La ley es presentada con el objetivo de exaltar, promocionar, incentivar, proteger y reconocer las industrias creativas. Estas son entendidas como “aquellas
industrias que generan valor en razón de sus bienes y servicios, los
cuales se fundamentan en la propiedad intelectual”.
Más
concretamente nos habla de los sectores editoriales, audiovisuales,
fonográficos, de artes visuales, de artes escénicas y espectáculos, de
turismo y patrimonio cultural material e inmaterial, de educación
artística y cultural, de diseño, publicidad, software de contenidos,
moda, agencias de noticias y servicios de información, y educación
creativa.
Objetivos
- Fomentar la financiación para un correcto desarrollo de las economías creativas. Se abrirán líneas de crédito a los artistas, a largo plazo y con mejores condiciones.
- Promoción de la formación en disciplinas culturales y creativas. El Gobierno prevé incrementar las becas y los créditos.
- Convertir a las industrias creativas en un generador de empleo de calidad y un motor de desarrollo.
- Triplicar las exportaciones de bienes y servicios creativos.
- Construcción de agendas de “ciudades creativas”. Crear una red de infraestructuras urbanas para mejorar los planes culturales territoriales.
Pasos a seguir
- El Departamento Administrativo Nacional de Estadística, junto con los entes territoriales realizarán estudios periódicos de la situación de las industrias creativas para adaptar los planes a seguir.
- Creación del Consejo Nacional de la Economía Naranja, el cual promoverá el fortalecimiento de las instituciones públicas, privadas y mixtas, para la protección de los creadores.
- Promoción de incentivos fiscales para personas o empresas que ejerzan patrocinio o mecenazgo.
- Posibilidad de sitiar ciertas zonas temporales para el correcto desarrollo de festivales y carnavales.
La estrategia de las 7i
Para poner en práctica y hacer efectiva la ley, el Gobierno ha creado una estrategia que se basa en los siguientes puntos:
-
Información:
los agentes culturales deben informase de los cambios que se producen
en la economía para poder conseguir los mejores beneficios posibles.
-
Instituciones:
son entendidas como un mecanismo de cooperación y coordinación dentro
de la Economía Naranja. Sus objetivos son conseguir un desarrollo
artístico y promover un acceso más amplio a la cultura.
-
Industria:
ésta debe entender la necesidad de hablar de dinero y conocer las
herramientas necesarias lo antes posible. Sin embargo, la ley no olvida
las peculiaridades del sector y de su naturaleza compleja. Por ello,
apoya una política pública que cree convergencias entre las iniciativas
privadas y públicas, así como fondos para la investigación y la creación
de empresas.
-
Infraestructuras:
se trata de crear una red de construcciones con las que se pueda poner
en contacto a los artistas y sus audiencias. Esto no solo puede darse
físicamente, si no también a través de las relaciones humanas, en las
cuales tiene una gran importancia las nuevas tecnologías. Es por ello,
que la ley incluye la necesidad de una política de “alfabetismo
digital”.
-
Integración:
la estrategia tiene como objetivo conseguir una mayor exportación a
través de explotar los nichos de mercado creados por Internet.
-
Inclusión:
consiste en aprovechar las industrias creativas para la regeneración
del tejido social y crear empleos a través de microcréditos y su
articulación con proyectos comunitarios de participación.
-
Inspiración: proporcionar al creativo el tiempo y la formación necesaria para la realización de su trabajo.
13 oct 2017
Triángulo de Sierpinski
El matemático polaco
Waclaw Sierpinski introdujo este fractal en 1919. Partamos (iteración
n=0) de la superficie de un triángulo equilátero de lado
unidad. Seguidamente (iteración n=1) tomemos los puntos medios de
cada lado y construyamos a partir de ellos un triángulo equilátero
invertido de lado 1/2. Lo recortamos. Ahora (iteración n=2) repetimos
el proceso con cada uno de los tres triángulos de lado 1/2 que nos
quedan. Así que recortamos, esta vez, tres triángulos invertidos
de lado 1/4. En la figura animada observamos hasta cinco iteraciones sucesivas.
Si repetimos infinitamente el proceso obtendremos una figura fractal denominada
triángulo de Sierpinski.

Sierpinski diseñó
este monstruo para demostrar, entre otras cosas, que era posible construir
una curva que se "cruzaba" consigo misma en todos sus puntos ...
Podemos hacer construcciones semejantes al triángulo de Sierpinski en 3 dimensiones con tetraedros. @
El triángulo de Sierpinski
se puede descomponer en tres figuras congruentes. Cada una de ellas con
exactamente la mitad de tamaño de la original. Si doblamos el tamaño
de una de las partes recuperamos el triángulo inicial. El triángulo
de Sierpinski está formado por tres copias autosimilares
de él mismo. Decimos que es autosimilar.

En realidad la autosimilaridad es
más profunda. Cada una de las copias puede descomponerse a su vez
de tres copias autosimilares (un total de nueve). Y a partir de cualquiera
de ellas, aumentando su tamaño en un factor 4 recuperamos el original.
En general, podemos dividir el triángulo en 3n piezas autosimilares que aumentadas
en un factor 2n
nos devuelven la figura inicial. Este tipo de autosimilaridad a todas las
escalas es el sello identificativo de un fractal.
Esta propiedad ha sido utilizada
con astucia en ingeniería. Un ejemplo reciente son las antenas fractales. El diseño
de antenas se ejecuta en gran medida por tanteo. Muchas antenas están
compuestas por una distribución de pequeñas antenas. Si la
distribución es regular, la antena presenta alto rendimiento y si es
aleatoria ofrece robustez. Parece que un diseño fractal como el de
la figura combina ambas propiedades. En el caso de un solo hilo, siguiendo
una forma fractal, al doblar se consigue empaquetar más hilo en el
mismo espacio y la forma dentada genera capacitancia e inductancia extra.

En este capítulo solo presentamos
ejemplos de fractales estrictamente autosimilares. Como veremos más
adelante esta autosimilaridad puede ser no perfecta, como en el caso del
conjunto de Mandelbrot, o estadística, como en el caso de las costas
terrestres.
Podemos hacer construcciones semejantes al triángulo de Sierpinski en 3 dimensiones con tetraedros. @
11 oct 2017
ANTENA YAGI
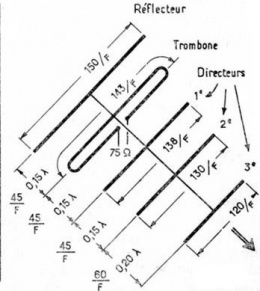
La antena Yagi es una antena direccional inventada por el Dr. Hidetsugu Yagi de la Universidad Imperial de Tohoku y su ayudante, el Dr. Shintaro Uda (de ahí al nombre Yagi-Uda). En esta antena sobresale la invención de quitar la tierra a las ya convencionales antenas (groundbreaking), lo cual produjo que mediante una estructura simple de dipolo, combinado con elementos parásitos, conocidos como reflector y directores, se lograra construir una antena de muy alto rendimiento.
En esencia, una antena es un sistema conductor metálico capaz de radiar y recibir ondas electromagnéticas, y una guía de onda es un tubo metálico conductor por medio del cual se propaga energía electromagnética de alta frecuencia, por lo general entre una antena y un transmisor, un receptor, o ambos. Una antena se utiliza como la interface entre un transmisor y el espacio libre o el espacio libre y el receptor. Una guía de onda, así como una línea de transmisión, se utiliza solo para interconectar eficientemente una antena con el transceptor. Una antena acopla energía de la salida de un transmisor a la atmósfera de la Tierra o de la atmósfera de la Tierra a un receptor. Una antena es un dispositivo recíproco pasivo; pasivo en cuanto a que en realidad no puede amplificar una señal, por lo menos no en el sentido real de la palabra (sin embargo, una antena puede tener ganancia), y recíproco en cuanto a que las características de transmisión y recepción son idénticas, excepto donde las corrientes de alimentación al elemento de trasmisión.
Las antenas yagi presentan dos tipos de elementos:
- Elementos de excitación. (Dipolo) Pueden ser activos o excitados, estos se conectan directamente a la línea de transmisión y reciben potencia de la fuente.
- Elementos parásitos. No se conectan a la línea de transmisión y reciben la energía a través de la inducción mutua. Estos elementos se clasifican en Reflectores y Directores.
Reflector. Elemento parásito más largo que el elemento de excitación. Reduce la intensidad de la señal que está en su dirección e incrementa la que está en dirección del dipolo.
Director(es). Elemento(s) parásito(s) más corto(s) que su elemento de excitación. Incrementa(n) la intensidad del campo en su dirección y la reduce(n) a la dirección del reflector.
Calculos de una antena Yagi.
En las antenas de 2 a 4 elementos, la separación aproximada es de 0.15 a 0.2 λ, en algunos casos se logra una ganancia mayor si el segundo director esta 0.25 λ del primero, y aun mayor, separando el tercero y cuarto elementos hasta un máximo de 0.4 λ.
Otro factor importante es la ganancia ya que esta aumenta rápidamente con pocos elementos y lentamente para un número mayor. Con un diagrama de 2 elementos (1 director, dipolo y un reflector) la ganancia es de 5 a 7 dB, con 5 es aproximadamente de 10 dB y de 8 elementos de unos 12 dB, por esta razón no se diseñan antenas Yagi de mas de 12 a 15 elementos.
Las formulas para el diseño de una antena Yagi son las siguientes:
Por lo general, las antenas se diseñan para una sola frecuencia, tomando por lo general la frecuencia central de la banda de frecuencia deseada.
Teniendo lo anterior, se calcula la longitud de onda para antena, que este caso sera para una frecuencia de 519.25 MHz, misma que se utiliza para la transmisión del canal 22.
Utilizando las formulas se calculan las logitudes del reflector, dipolo y primer director.
Utilizando la siguiente tabla se decide cuantos directores se quieren usar.
N° Directores
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Ganancia [dB]
|
9
|
9.5
|
10
|
11
|
12
|
13.5
|
15
|
15.5
|
16
|
RDipolo
|
80
|
76
|
72
|
64
|
56
|
50
|
44
|
40
|
38
|
2° Director
3° Director
4° Director
5° Director
6° Director
7° Director
8° Director
9° Director
10° Director
|
n
|
n
p
|
n
p
q
|
n
p
q
s
|
m
n
p
q
s
|
m
n
n
p
q
s
|
m
n
n
p
p
q
s
|
m
n
n
p
p
q
q
s
|
m
n
n
p
p
q
q
s
s
|
Por ultimo se calcula la separación que se utiliza.
9 oct 2017
ANTENA PARABOLICA

En las antenas parabólicas transmisoras, la así llamada parábola refleja las ondas electromagnéticas generadas por un dispositivo radiante que se encuentra ubicado en el foco del paraboloide. Los frentes de onda inicialmente esféricos que emite ese dispositivo se convierten en frentes de onda planos al reflejarse en dicha superficie, produciendo ondas más coherentes que otro tipo de antenas.En las antenas receptoras el reflector parabólico se encarga de concentrar en su foco, donde se encuentra un detector, los rayos paralelos de las ondas incidentes.
Tipos De Antenas Parabólicas
Atendiendo a la superficie reflectora, pueden diferenciarse varios tipos de antenas parabólicas, los más extendidos son los siguientes:
La antena parabólica de foco centrado o primario
La antena parabólica de foco desplazado u offset
La antena parabólica Cassegrain
La antena plana
Ecuaciones para calculo de una antena parabólica.
Las ecuaciones para la superficie del reflector son:

Donde ρ es la distancia del foco al punto de reflexión sobre la superficie parabólica y f la distancia del vértice al foco o distancia focal.
La profundidad del reflector desde el vértice de la parábola hasta el punto de intersección entre las rectas comprendidas por el eje focal y la línea que une los extremos de las parábola es:

Donde D es el diámetro y f es la longitud focal.
El ángulo comprendido entre el eje focal y la línea que une el foco con un extremo de la parábola es:

Directividad y Ganancia:
La máxima directividad que puede obtener un reflector parabólico se puede calcular aproximadamente mediante la siguiente expresión:

Para un reflector parabólico de boca circular, el valor de A, área de captación es:
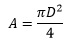
Donde D, es el diámetro de la apertura, con lo que la directividad queda:

La ganancia de una antena parabólica con apertura con respecto al dipolo λ/2, es:

La directividad de una antena parabólica con una apertura cuadrada sería:

Y su respectiva ganancia con respecto al dipolo λ/2 es:

Ejemplo.
Diseñar una antena parabólica con un diámetro de 3m, una eficiencia de 60% y una frecuencia de 4GHz

Atendiendo a la superficie reflectora, pueden diferenciarse varios tipos de antenas parabólicas, los más extendidos son los siguientes:
La antena parabólica de foco centrado o primario
La antena parabólica de foco desplazado u offset
La antena parabólica Cassegrain
La antena plana
Ecuaciones para calculo de una antena parabólica.
Las ecuaciones para la superficie del reflector son:

Donde ρ es la distancia del foco al punto de reflexión sobre la superficie parabólica y f la distancia del vértice al foco o distancia focal.
La profundidad del reflector desde el vértice de la parábola hasta el punto de intersección entre las rectas comprendidas por el eje focal y la línea que une los extremos de las parábola es:

Donde D es el diámetro y f es la longitud focal.
El ángulo comprendido entre el eje focal y la línea que une el foco con un extremo de la parábola es:

Directividad y Ganancia:
La máxima directividad que puede obtener un reflector parabólico se puede calcular aproximadamente mediante la siguiente expresión:

Para un reflector parabólico de boca circular, el valor de A, área de captación es:
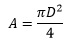
Donde D, es el diámetro de la apertura, con lo que la directividad queda:

La ganancia de una antena parabólica con apertura con respecto al dipolo λ/2, es:

La directividad de una antena parabólica con una apertura cuadrada sería:

Y su respectiva ganancia con respecto al dipolo λ/2 es:

Ejemplo.
Diseñar una antena parabólica con un diámetro de 3m, una eficiencia de 60% y una frecuencia de 4GHz

VISITA RADIO Y TV HIDALGO
En
la visita a la radio y television de hidalgo, pudimos observar el
proceso de creación de la transmision de la señal de Radio y Tv,
entendiendo que en cada oficina/departamento tiene que pasar por ciertos
protocolos para así obtener la señal más optima, tanto como en una
señal en vivo y un programa previamente grabado.
Primeramente se crea la señal, que en este caso sería audio y video, de ahí pasamos al cuarto de contro de video y de audio, para así procesar las señales y tratar de que estén lo mas aptas posibles para asi salír al "master" que es ahí dónde se le da el formato necesario para de ahi salir a la antena transmisora hacia el satelite con aproximaxdamente una frecuencia de 6 GHz de subida por 3 GHz de bajada, para poder llegar de la manera mas optima y con la potencia suficiente para llegar hasta el satelite y de ahi, poder regresar el mismo satelite la señal hacia las antenas que propagan la señal terrestre. De manera similar con la radio...
Una visita muy interesante.
Primeramente se crea la señal, que en este caso sería audio y video, de ahí pasamos al cuarto de contro de video y de audio, para así procesar las señales y tratar de que estén lo mas aptas posibles para asi salír al "master" que es ahí dónde se le da el formato necesario para de ahi salir a la antena transmisora hacia el satelite con aproximaxdamente una frecuencia de 6 GHz de subida por 3 GHz de bajada, para poder llegar de la manera mas optima y con la potencia suficiente para llegar hasta el satelite y de ahi, poder regresar el mismo satelite la señal hacia las antenas que propagan la señal terrestre. De manera similar con la radio...
Una visita muy interesante.

6 oct 2017
POLARIZACIÓN DE ANTENAS
La polarización de una antena es la polarización de la onda radiada por dicha antena en una dirección dada.
La polarización de una onda es la figura geométrica determinada por el extremo del vector que representa al campo eléctrico en función del tiempo, en una posición dada. Para ondas con variación sinusoidal dicha figura es en general una elipse. Hay una serie de casos particulares.
Si la figura trazada es una recta, la onda se denomina linealmente polarizada, si es un círculo circularmente polarizada.
El sentido de giro del campo eléctrico, para una onda que se aleja del observador, determina si la onda está polarizada circularmente a derechas o a izquierda. Si el sentido de giro coincide con las agujas del reloj, la polarización es circular a derechas. Si el sentido de giro es contrario a las agujas del reloj, la polarización es circular a izquierdas. El mismo convenio aplica a las ondas con polarización elíptica.
Se define la relación axial de una onda polarizada elípticamente, como la relación entre los ejes mayor y menor de la elipse de polarización. La relación axial toma valores comprendidos entre 1 e infinito.
Los campos se pueden representar en notación fasorial. Para determinar la variación temporal es suficiente con determinar el valor real de cada una de las componentes. Los ejemplos que se citan a continuación son para ondas planas que se propagan en la dirección del eje z.
Las expresiones siguientes representan campos con polarización lineal

Las expresiones siguientes representan campos con polarización circular, la primera a izquierdas y la segunda a derechas

Finalmente los siguientes ejemplos corresponden a polarizaciones elípticas

Se produce una polarización lineal cuando las fases de dos componentes ortogonales del campo eléctrico difieren un múltiplo entero de p radianes. Se produce polarización circular cuando las amplitudes son iguales y la diferencia de fase entre las componentes es p/2 o 3p/2. La polarización es elíptica en los demás casos.
Cualquier onda se puede descomponer en dos polarizaciones lineales ortogonales, sin más que proyectar el campo eléctrico sobre vectores unitarios orientados según dichas direcciones. Aplicando el mismo principio, cualquier onda se puede descomponer en dos ondas polarizadas circularmente a derechas o izquierdas.
Por ejemplo la siguiente expresión representa una onda polarizada elípticamente a derechas, con relación axial 3.

Se puede descomponer en dos ondas polarizadas linealmente de amplitudes 3 y –1, o bien en dos ondas porlarizadas circularmente a derechas e izquierdas

Resolviendo el siguiente sistema de ecuaciones se determinan los valores de A y B

Los valores de A=2 y B
La polarización de una onda es la figura geométrica determinada por el extremo del vector que representa al campo eléctrico en función del tiempo, en una posición dada. Para ondas con variación sinusoidal dicha figura es en general una elipse. Hay una serie de casos particulares.
Si la figura trazada es una recta, la onda se denomina linealmente polarizada, si es un círculo circularmente polarizada.
El sentido de giro del campo eléctrico, para una onda que se aleja del observador, determina si la onda está polarizada circularmente a derechas o a izquierda. Si el sentido de giro coincide con las agujas del reloj, la polarización es circular a derechas. Si el sentido de giro es contrario a las agujas del reloj, la polarización es circular a izquierdas. El mismo convenio aplica a las ondas con polarización elíptica.
Se define la relación axial de una onda polarizada elípticamente, como la relación entre los ejes mayor y menor de la elipse de polarización. La relación axial toma valores comprendidos entre 1 e infinito.
Los campos se pueden representar en notación fasorial. Para determinar la variación temporal es suficiente con determinar el valor real de cada una de las componentes. Los ejemplos que se citan a continuación son para ondas planas que se propagan en la dirección del eje z.
Las expresiones siguientes representan campos con polarización lineal

Las expresiones siguientes representan campos con polarización circular, la primera a izquierdas y la segunda a derechas

Finalmente los siguientes ejemplos corresponden a polarizaciones elípticas

Se produce una polarización lineal cuando las fases de dos componentes ortogonales del campo eléctrico difieren un múltiplo entero de p radianes. Se produce polarización circular cuando las amplitudes son iguales y la diferencia de fase entre las componentes es p/2 o 3p/2. La polarización es elíptica en los demás casos.
Cualquier onda se puede descomponer en dos polarizaciones lineales ortogonales, sin más que proyectar el campo eléctrico sobre vectores unitarios orientados según dichas direcciones. Aplicando el mismo principio, cualquier onda se puede descomponer en dos ondas polarizadas circularmente a derechas o izquierdas.
Por ejemplo la siguiente expresión representa una onda polarizada elípticamente a derechas, con relación axial 3.

Se puede descomponer en dos ondas polarizadas linealmente de amplitudes 3 y –1, o bien en dos ondas porlarizadas circularmente a derechas e izquierdas

Resolviendo el siguiente sistema de ecuaciones se determinan los valores de A y B

Los valores de A=2 y B
4 oct 2017
ANTENA HERTZ
Una antena es un dispositivo formado por un conjunto de conductores que, unido a un generador, permite la emisión de ondas de radio frecuencia, o que, conectado a una impedancia, sirve para captar las ondas emitidas por una fuente lejana para este fin existen diferentes tipos:
Antena Colectiva: Antena receptora que, mediante la conveniente amplificación y el uso de distribuidores, permite su utilización por diversos usuarios
Antena de Cuadro: Antena de escasa sensibilidad, formada por una bobina de una o varias espiras arrolladas en un cuadro, cuyo funcionamiento bidireccional la hace útil en radiogoniometría
Antena de Reflector o Parabólica: Antena provista de un reflector metálico, de forma parabólica, esférica o de bocina, que limita las radiaciones a un cierto espacio, concentrando la potencia de las ondas; se utiliza especialmente para la transmisión y recepción vía satélite.
Antena Lineal: La que está constituida por un conductor rectilíneo, generalmente en posición vertical.
Antena Multibanda: La que permite la recepción de ondas cortas en una amplitud de banda que abarca muy diversas frecuencias
Dipolo de Media Onda: El dipolo de media onda lineal o dipolo simple es una de las antenas más ampliamente utilizadas en frecuencias arriba de 2MHz. En frecuencias abajo de 2 MHz, la longitud física de una antena de media longitud de onda es prohibitiva. Al dipolo de media onda se le refiere por lo general como antena de Hertz.
Una antena de Hertz es una antena resonante. O Sea, es un múltiplo de un cuarto de longitud de onda de largo y de circuito abierto en el extremo más lejano. Las ondas estacionarias de voltaje y de corriente existen a lo largo de una antena resonante.

La figura anterior podemos observar las distribuciones de corriente y voltaje ideales a lo largo de un dipolo de media onda. Cada polo de la antena se ve como una sección abierta de un cuarto de longitud de onda de una linea de transmisión. Por lo tanto en los extremos hay un máximo voltaje y un mínimo de corriente y un mínimo de voltaje y un máximo de corriente en el centro. En consecuencia, suponiendo que el punto de alimentación esta en el centro de la antena, la impedancia de entrada es Eminimo / Imaximo y un valor mínimo. La impedancia en los extremos de la antena de Emaximo / Iminimo y un valor máximo.
La figura siguiente muestra la curva de impedancia para un dipolo de media onda alimentado en el centro.

La impedancia varia de un valor máximo en los extremos de aproximadamente 2500 W a un valor mínimo en el punto de alimentación de aproximadamente 73 W (de los cuales entre 68 y 70 W es la impedancia de radiación).
El patrón de radiación de espacio libre para un dipolo de media onda depende de la localización horizontal o vertical de la antena con relación a la superficie de la tierra.
La figura siguiente muestra el patrón de radiación vertical para un dipolo de media onda montado verticalmente. Observese que los dos lóbulos principales que irradian en direcciones opuestas están en ángulo derecho a la antena, los lóbulos no son círculos, se obtienen solo en el caso ideal donde la corriente es constante a todo lo largo de la antena, y esto es inalcanzable en una antena real.

Suscribirse a:
Comentarios (Atom)